It’s not Magic, it’s Math

Hi everyone! I hope you enjoyed my brief series on Data Science. There was much more I wanted to cover, and perhaps I’ll dig into some details later, but I’m trying to keep to my promise of going just deep enough to get a good idea of what’s going on without becoming an expert. I’m extremely excited to talk to you about this next topic in this new series of posts: Artificial Neural Networks.

Artificial Neural Networks (ANNs) have become a cornerstone of modern artificial intelligence, powering everything from voice assistants and facial recognition systems to recommendation engines and autonomous vehicles. I think by now we all know that ANNs are extremely powerful tools, but doesn’t it all seem a little too magical? “Oh yeah, we just gathered a bunch of data and trained a neural network on it and now it can predict things with incredible accuracy.” Huh? How does THAT work? “Oh you just show it a bunch of data over and over again and eventually it learns.” I don’t know about you but for my part, after all the “ooo! ahhh!” I was left thinking that this was hocus-pocus and I wasn’t very comfortable with it. So I got down to learning, and here is how my brain made sense of it.

I started with the basics, focusing on the most essential building block of an ANN: the single neuron. Let’s do that together here. By understanding how a single neuron works and how it can identify linear relationships within data, we’ll lay the groundwork for comprehending more complex neural network architectures. We’ll walk through the training process step-by-step, ensuring that each concept is clear and approachable.

As we progress through this series, we’ll gradually build upon these basics, moving from single neurons to multi-layered networks, and eventually to specialized architectures like Convolutional Neural Networks (CNNs). My goal is to provide you with a working understanding of ANNs, enabling you to see beyond the magic and appreciate the powerful mathematics and algorithms that drive these systems.

I can’t promise that there will be no math at all, but I really don’t think a whole lot of math is needed to get a pretty solid grasp on things. And the cool thing is that once we have wrapped our heads around ANNs, we can move on to understanding the new an exciting world of LLMs and generative AI systems. We are slowly but surely inching our way there.

Some Quick Basics

Before we get started, I think it’s important to just take a brief moment to talk about neural networks and neurons and why we call them that and how they generally work. You probably already know most of this. I certainly had been exposed to enough talk about neural networks to get the basic gist of how they were analogous to biological neurons. But I’m not a neurosurgeon, so even my understanding of biological neurons was whatever I remembered from college biology.

A wonderful resource for learning about neural networks from the ground up is this free online E-book called Neural Networks and Deep Learning. I highly recommend it because it’s very well written and approachable.

We all know that our brains are made up of a bunch of neurons that are connected to each other. As we navigate the world, our senses are stimulated by what we encounter, and electrochemical signals are sent through our nervous system into this wad of neurons. Over time, as we are exposed to sensations over and over again, some neural pathways become well-travelled. And some associations between various neurons in our brain also become reenforced. We get used to certain sensations and we become very adept at recognizing them. Similarly, at first when we are stimulated with don’t know how to respond. We respond in all sorts of weird ways. Think about the strange look you get from a baby that is just learning to use her eyes. Eventually though, she recognizes you, and eventually she smiles back at you. And when that happens, she gets hugs and kisses, which teaches her that smiling is good. I’m over-simplifying here (and as a student of philosophy of mind, I am cringing at myself a little too) but this is the rough idea.

Back in the 1950s, some scientists started to experiment with modeling how neurons in our brains worked using mathematical relationships. A biological neuron looks like this:

On either end of this, at the inputs and outputs, just imagine more neurons, with all their spidery dendrites and axons. So the scientists looked at this and thought “OK.. so basically a neuron gets a bunch of input, somehow combines that input and generates some output.” The output is based on the input in some way. The neuron does “something” with the input. Mathematically, this actually looks like a function that takes inputs and generates outputs. So maybe if you had a bunch of really simple mathematical functions that did really simple things with inputs to turn them into outputs, and you connected them all to each other, they might behave like a brain.

There have been a few variations on this line of thinking, and the mathematical “neuron” has evolved, but we’ve ended up with something like this:

I’ll explain all the little parts of this, but basically you have inputs on the left (the Xs) and then some stuff happens in the middle (the blue and purple parts) and then you have the output (o). So really, as you can imagine, the key is what’s happening in the middle. And this is the part that seems magical, because what you get told is that in the beginning the neuron is just doing random things in the middle. It just eventually LEARNS to do the right thing after being exposed to a lot of data. My brain REBELLED at this notion. I HAD to understand this.

The Single Neuron

Let’s simplify this problem as much as we can. We are going to try to understand how a single neuron works. A very very simple neuron. Let’s reduce the number of inputs to just ONE input. And let’s have just ONE output. So you basically have this:

In more mathematical terms, if x in your input and y is your output, “do something” is called a function. This function takes x as input and produces y as output. And you write that f(x) = y. That’s it. That’s the neuron. So if I want to, say convert from degrees centigrade to degrees Fahrenheit, I let x = my degrees centigrade, run x through f and I get my degrees Fahrenheit in y. Magic.

But wait.. how does f() do that? Ah yes. There is the rub. We have to actually define f. We have to say what f does. And here was the first insight that lead to a lot of good stuff. For a neuron with a single input, f is: wx + b. That is, f produces a value of y by multiplying x by something and adding something to it. The w is something called a ‘weight’ and b is called the ‘bias’. I will explain more on that later, but it helps to remember that neurons can have multiple inputs and each input can have a different weight. That basically tells the neuron to pay more attention to some of its inputs than others. It’s a bit like how most people trust their eyes more than their noses and dogs trust their noses more than their eyes. The bias is also important but will be easier to explain later.

Anyway, if you remember some math from school, the formula might look familiar. It’s the y-intercept notation for a linear function. It’s commonly written as y = mx +b, where m is the slope and b is the y-intercept. If you know the slope of a line and you know where this line intercepts the y-axis, you can calculate all values of y for all values of x.

That’s the whole game! Finding the right values of w and b. When we say that the neuron starts out working randomly and then eventually learns how to get the answer right, we are talking about starting with random values of w and b, and gradually changing them until we get closer and closer to the right answer. This seems like a good time to talk about training data.

Training a Model

When we build ANNs, as we just discovered, they are initialized with random values of w and b. We want to gradually find the best values of w and b, and allow our “wx + b” function (sometimes called the Transfer Function) to produce the best results. If we are converting from degrees C to degrees F, we want to find values of w and b that will give us the right conversion every time. Of course we know what those values are, but we don’t want to give them to the neuron. We want the neuron to figure them out. How does this work?

Well, let’s say our neuron starts out with w being 8 and b being 3. So the function would be y = 8x + 3. So if I give it a value of 10 degrees C, it would tell me that this is 83 degrees F. That is completely wrong. The answer should actually be 50. In this case I was way off.. off by 33. What if I feed it 0 degrees C? Then the neuron would say: 8(0) + 3 = 3. That is also way off. It should have been 32. So I’m off by 29. What about 20 degrees C? Neuron says 163. Correct answer is 86. I’m off by 77. That’s terrible.

What I’ve just done is a single iteration of training. I had input data (10, 0, 20) as well as expected output data (50, 32, 86). I fed the input data to my neuron, and compared the generated output (83, 3, 163) to the expected output and calculated my errors (33, 29, 77).

I can now take what I’ve learned about my errors by perhaps taking the average of all my errors (or, more commonly square root of the average of the square of each error, called the Root Mean Squared Error or RMSE) and tell my system: “the neuron failed. Here is how badly it failed”. So imagine I have a piece of software (call it the adjuster) whose job it is to keep track of these errors, and change the values of w and b.. And the adjuster would look at the RMSE and change the values of w and b a little. It doesn’t really know how to change the values. But it keeps track of the effect of changing the values. It might be easier to show this in python:

from math import sqrt
# A function to calculate the root mean squared error for some set of results
# and expected results.
def rmse(results, expected_results):
    sum_of_squared_errors = 0
    for result, expected_result in zip(results, expected_results):
        sum_of_squared_errors += ((result - expected_result) ** 2)
    return(sqrt(sum_of_squared_errors / len(results)))

# This is the Transfer function of the Neuron
def neuron_function(x, w, b):
    return(w*x + b)

input_data = [10, 0 , 20]
expected_results = [50, 32, 86]

w = 8
b = 3
results = [y for y in [neuron_function(x, w, b) for x in input_data]]
print("Results: ",results)
print("Expected: ", expected_results)
print("RMSE: ", rmse(results,expected_results),"\n")

# Here some sort of Adjuster takes the RMSE value and comes up with
# Another set of values for w and b. (We will talk about how this works later.)
w = 5
b = 6
results = [y for y in [neuron_function(x, w, b) for x in input_data]]
print("Results: ",results)
print("Expected: ", expected_results)
print("RMSE: ", rmse(results,expected_results), "\n")

If you run this: you will get this output:

Results:  [83, 3, 163]
Expected:  [50, 32, 86]
RMSE:  51.18267936193519 

Results:  [56, 6, 106]
Expected:  [50, 32, 86]
RMSE:  19.252705437591537 

As you can see, changing w and b from 8,3 to 5,6 decreased the amount of error in our outputs. We are still off, but closer. This is the training process. We run through the neuron with input, knowing what the expected output should be, then we compare what we got with what we expected, and we feed information about the error rate to some piece of software that uses it to make tweaks to the values of w and b, trying to get a better error value next time. If the error value keeps decreasing, it keeps doing what it’s doing. If the error value increased, it either backtracks to tries something else. For example, maybe it tries changing only w, or only b. Maybe it takes big steps when changing the values, maybe it takes little ones.

Gradient Descent

The process of using the error value to make tweaks to the w (weight) and b (bias) values (jointly called “parameters”) is called “gradient descent”. What this process does is it plots the error values for different parameter values it has tried, and it monitors the slope of the error curve (or surface, since w and b make a two-dimensional space). The gradient descent will change the values of the metrics in a way that allows it to find the point where the slope of the error curve bottoms out. Kind of like the way water makes its way to the drain in a sink.. the lowest point. It follows the slope down to the drain. This, like training, is not magical. It’s mathematical. But since I promised not to get too mathy, I won’t dive into how the algorithm works. Feel free to read about it here.

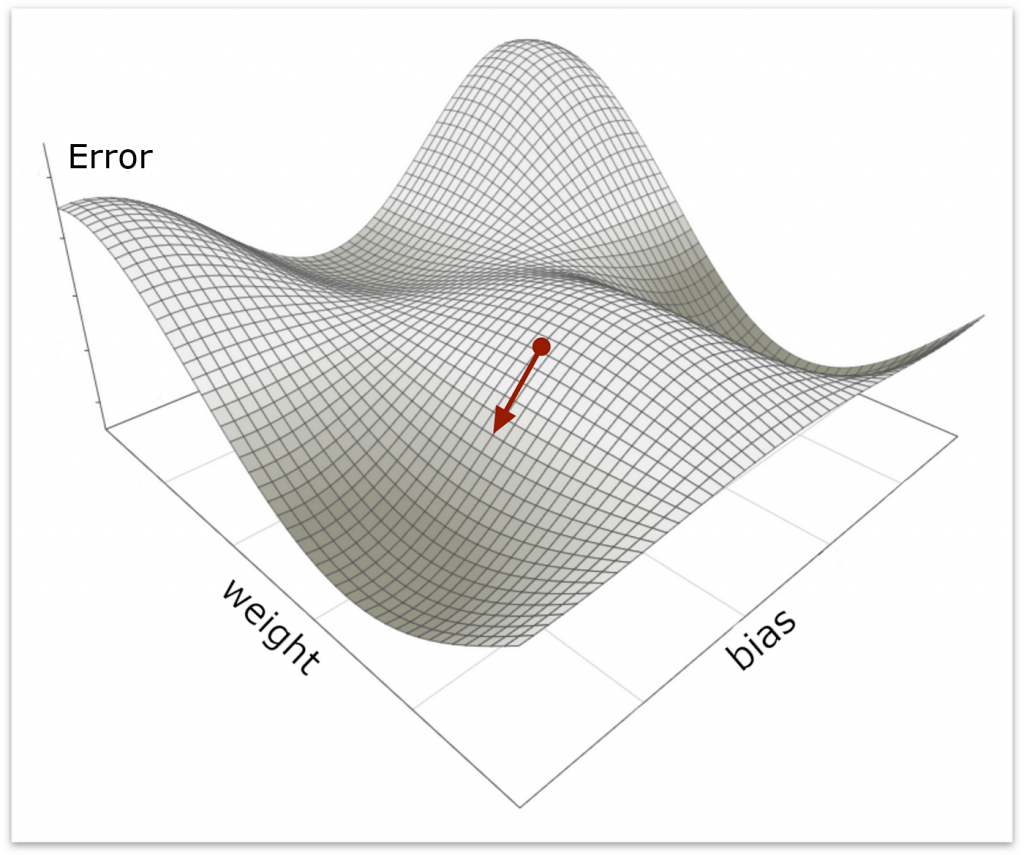
So now we can start to imagine how this works. In my example above, we only had THREE data points, and we only did two test iterations, and we already improved the results. Imagine that we had 1000 data points and that we ran the test 50 times. Each time, we got a value for RSME and each time we used it to guess which way we should tweak our metrics. You can imagine that we would start to zero in on the best values of w and b, even though we are essentially doing it by stumbling around in the dark with only “getting warmer” and “getting colder” as a guide.

By the way, in case you didn’t remember, the correct values for w and b to convert from centigrade to Fahrenheit are w = 1.8 and b = 32. So F = 1.8C + 32. Our guesses for w and b were still way off, but we were moving in the right direction!

In an upcoming post, when I talk about TensorFlow and show you how to build neural networks, you will build this experiment yourself and train it and see the magic happen. But hopefully you can now see past the magic and understand that this is really just a bunch of little numerical nudges oriented by a measurement of the difference between an obtained result and an expected one.

Other Types of Data

There are two other important concepts I want to talk about briefly, even though they will come up again many times as we delve into this topic: Validation and Testing.

Usually when we have a bunch of data that we can pass to our neural network in order to train it, we want to hold some of that data back for validation and testing. What’s the difference between them?

• Training data: A bunch of inputs and expected outputs. You feed the inputs to the system and compare the outputs to the expected outputs. You measure the error and use that measurement to make changes to the metrics before running through the same data again and seeing if the results are now better.
• Validation data: This is used to evaluate the model during training, helping to tune hyperparameters and prevent overfitting. Unlike training data, the errors on validation data are not used to update the model’s weights. If the model performs significantly better on training data than on validation data, it indicates overfitting, meaning the model has learned the training data too well and fails to generalize. Over-fitting is a little like learning to pass the state exam without really understanding the concepts. We’ll talk more about that in a future post. I’ve also not told you what a hyperparameter is yet. There are several and we will discuss them later, but generally they are settings for 1) how to conduct testing and adjusting 2) what the model should look like and how it should treat data.
• Testing data: It’s also the same kind of data as training data. It’s just held back to perform testing. You run the testing data through the model just one time instead of multiple times like you do training data. And you are checking whether the model is doing a good job or not. You use testing data to score the model’s performance and decide whether you want to re-train or change the model in some way to get better results.

Wrapping up

When I started learning about neural networks, understanding how the process of training a single neuron eventually leads to it producing real, reliable output (predictions), it was a major lightbulb moment. It took what was until then a fuzzy concept that I would blithely repeat in the appropriate context without truly understanding it, and crystallized it in my mind. And it made understanding the work that was to come feel less like an exercise in voodoo magic and more like a really well thought out way to leverage powerful math without worrying about the details. The reason my learning journey passes through artificial neural networks is that when I watched those videos explaining what a Transformer is or how GPT works, the concepts were just beyond my reach. This lesson about a single neuron is what made the difference for me and I hope it’s done the same for you.

Next time, I will talk about building actual networks of these neurons and how these networks very quickly become extremely powerful. I’ll also introduce topics like activation functions and back propagation algorithms. I hope you’ll join me. In the mean time, as always, I invite you to join in the conversation!